高斯竞赛全解析：如何备考拿下TOP1%

五至八年级通常是一个孩子从幼年掌握的基本算术、逻辑和观察能力逐步提升到更加系统的数学能力的重要阶段。在北美针对这一阶段的数学竞赛有不少，例如AMC8、Gauss7/8、Kangaroo7/8、CNML、Caribou等。今天我们来简单聊一聊高斯 (Gauss) 竞赛。高斯竞赛是滑铁卢大学 (University of Waterloo) 旗下的CEMC (The Centre for Education in Mathematics and Computing) 主办的一系列数学竞赛中的入门级竞赛。

高斯竞赛分为7、8年级两套试卷，均为60分钟，其中7年级的题稍容易一些；每年5月中旬举办考试，有大约4万学生参加，其中大约千分之一左右的同学可以考到150分满分，前10%的分数线大约是120分左右。

与AMC8对比

两者都是针对8年级的数学竞赛（小于8年级的同学也是可以参加的），都是25题单选题；不同点在于，AMC8是40分钟考试时间，每题1分，总分25分，题目难度较为平均，最后5题较难；AMC8的题相对而言是更加正统的数学题，整套试卷的题目难度比较平均，没有像高斯竞赛sectoin A部分特别容易的送分题；考试的时间上Gauss比AMC8多出20分钟时间，因此Gauss竞赛的满分相比AMC8更容易拿到一些；高斯是60分钟考试时间，分A，B，C 3个section

section A共10题，每题5分

section B共10题，每题6分

section C共5题，每题8分

（总分50+60+40=150分）

由于2020年高斯(Gauss)竞赛因为疫情原因而取消了，我们拿2019年5月的高斯竞赛成绩与2018年11月的AMC8竞赛成绩（属于同一届学生参加的）进行比较。AMC8错6题还在top 1%而Gauss错6题(即使错的都是5分题，其实不太可能)已经掉出前8%。

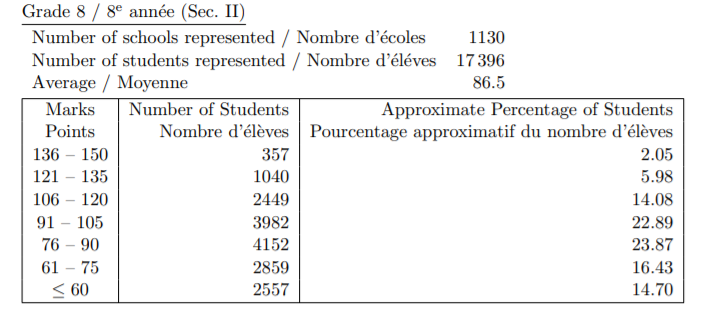
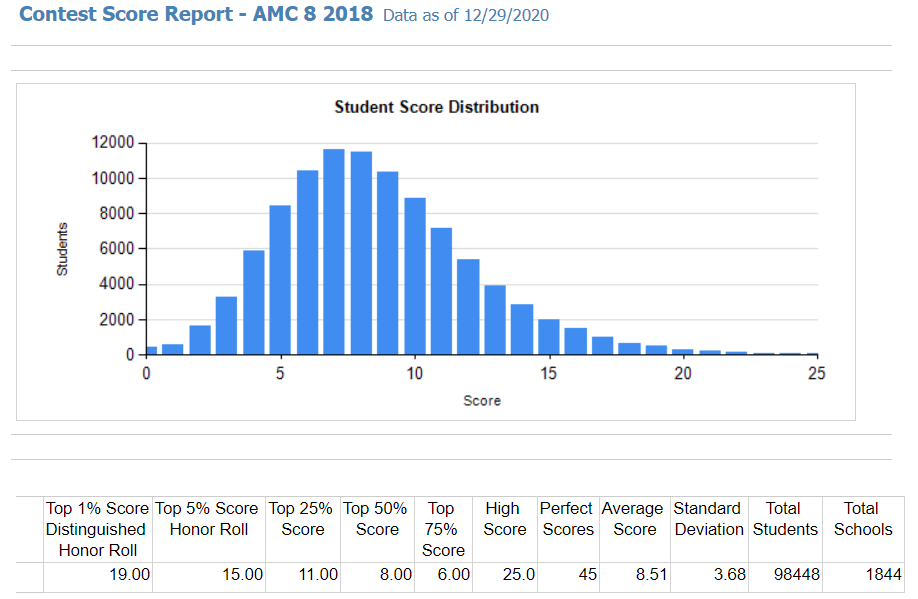
（官网截图）

高斯难度详解

Section A的题目是非常容易的，难题在于Section C的5题，尤其是最后2题；高斯竞赛的难题主要在Couting and Probability类的综合题上(类似排列组合的综合题型)；同时解题时没有特别的套路，通常是用枚举法加归纳法来思考问题；考察学生对各种情况是否考虑的准确及完备，而这类思维方式更接近计算机竞赛方向的思维模式。

如何备考

如果参加了AMC8竞赛的同学成绩不够理想，通过一段时间的培训和练习完全有希望在接下来的Gauss竞赛中取得更好的成绩。同AMC8竞赛一样，我们同样为冲击高斯竞赛高分的同学制定了平时训练的做题速度目标：

Part A: 10题，5分钟

Part B: 10题，20分钟

Part C: 前3题，6分钟，后2题各10分钟，剩余4分钟机动

（高斯竞赛主要难点在24，25题。平时训练时如果10~12分钟做不出来的，考试时这题基本上要失分。）

真题解析

01.2020年第25题

解析：首先我们要理解题目中讲到的这个数列的意思；这是一个只有2020项元素的数列，每个元素都是正整数，同时从第三个元素开始，每个元素的值是前2个元素之和；题目说了值为奇数的元素比值为偶数的元素多2倍以上。我们来枚举一下什么情况下奇数值的元素个数为偶数值的个数的2倍以上。根据两个数字之和的奇偶规律，其实只有4种基本情况：

因此，第一步我们枚举得出了A1，A2必须都是奇数，或者是A1为奇数，A2为偶数，这2种情况。下面我们看第二个条件：A1，A2都小于2m（m为正整数）。同样我们枚举一下，

根据上面的枚举情况，我们可以归纳一下规律，{A1，A2}组合中A1、A2都是奇数的情况是m2个，A1、A2是奇、偶的情况是m*(m-1)，所以总共是m*(2m-1)种情况；

题目说一共是2415种情况,所以2m2-m=2415=3*805=3*5*161=3*5*7*23；

通过十字相乘法来因式分解这个一元二次方程马上可以得出(2m+3*23)(m-5*7)=0，所以m的正整数解是35，选D。

解题感想：像这样的题没有什么难的规律或定理可以套用，主要解题方法就是通过枚举和归纳法来找出其中的规律。

02.2016年第25题

解析：基本上就是用等差数列和平均数的概念；我们把这个table看成二维数组[row, column]，最左上角的点是[1,1]，第一行第五列的点（即数值为18的点）我们叫[1,5]，右下角的点叫[5,5]。下面我们假设[1,1]的值是Y，这样我们利用平均数可以方便的得到[1,3]的值为9+Y/2，[5,3]的值是71-Y/2。

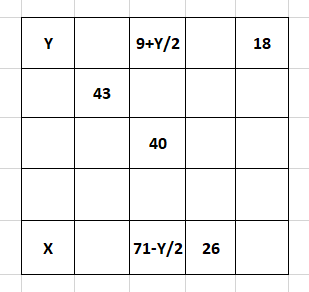
现在我们有X,Y两个变量。而最后一行，利用等差数列的公式我们已经可以得到第一个关系方程：

现在我们还有43这个点(即[2,2]这个点)的条件没有用上，同样用等差数列的知识，我们可以得到第二个关系方程：

Y+(X-Y)/4+49/2+Y/4=43*2

这样就变成了求解一个二元一次方程组。

71-Y/2=26-(26-X)/3；

Y+(X-Y)/4+49/2+Y/4=43*2；

最后解出X=110。所以X的数字之和是1+1+0=2，选B。

解题感想：同样，这题从难度上也不是特别难，不过没有特别的捷径。快速找到方便计算的元素点，列出关系式，是快速解题的关键。

数理化词汇

要想在竞赛中取得好成绩，基本的数学名词一定要总结清楚。比如今天我们例题中讲到的arithmetic sequence，就是我们常说的“等差数列”或者叫“算术数列”的意思。本次的出题者比较仔细，专门举例说明了一下。但是大部分情况下题目是不会解释常用名词术语的。比如大家知道mode（众数）在数列里代表什么意思吗？

环球U+为同学们准备了理科必备词汇本：

200+数理化生理科单词

20+基础练习题

快来联系规划师领取福利吧！

    欲了解更多雅思、托福、 SAT、SSAT、 COPE等语言类标准化考试培训课程及加拿大名校申请服务，欢迎就近至环球教育多伦多学校 - 北约克North York校区、列治文山Richmond Hill校区进行详细咨询，或访问多伦多环球教育唯一官方网站： http://toronto.gedu.org；

    同时您也可以扫描环球教育加拿大官方微信二维码，与雅思大神级名师互动问答，考前免费预测答疑，为您的考试保驾护航。 请致电官方咨询专线647-352-6616预约免费入学测评与试听服务。